Unleashing the Power of Linear Regression in Supervised Learning

Purple Artificial Intelligence Technology Business Instagram Post

In the realm of machine learning, supervised learning is one of the most widely-used techniques for predictive modeling. Linear regression, a simple yet powerful algorithm, is at the core of many supervised learning applications. In this blog post, we will delve into the basics of linear regression, its role in supervised learning, and how you can use it to solve real-world problems.

What is Linear Regression? Linear regression is a linear approach to modeling the relationship between a dependent variable and one or more independent variables. It aims to find the best-fitting line that describes the relationship between the input features (independent variables) and the target output (dependent variable). The primary goal of linear regression is to minimize the difference between the actual output and the predicted output, thereby reducing the prediction error. The Role of Linear Regression in Supervised Learning Supervised learning is a type of machine learning where the algorithm is trained on a labeled dataset, meaning each data point in the training dataset has a known output value. Linear regression is an essential supervised learning technique used for various purposes, such as:
  1. Predicting numerical outcomes: Linear regression is highly effective in predicting continuous numerical values, such as house prices, stock market trends, or sales forecasts.
  2. Identifying relationships: By analyzing the coefficients of the linear regression model, you can identify the strength and direction of relationships between input features and the target output.
  3. Feature selection: Linear regression can be used to identify the most significant features that contribute to the target output, enabling you to focus on the most crucial variables in your dataset.
To demonstrate the power of linear regression, let’s walk through a simple example by build a linear regression model to predict the prices of used cars in India, and generate a set of insights and recommendations that will help the business.

Context

There is a huge demand for used cars in the Indian Market today. As sales of new cars have slowed down in the recent past, the pre-owned car market has continued to grow over the past years and is larger than the new car market now. Cars4U is a budding tech start-up that aims to find footholds in this market.

In 2018-19, while new car sales were recorded at 3.6 million units, around 4 million second-hand cars were bought and sold. There is a slowdown in new car sales and that could mean that the demand is shifting towards the pre-owned market. In fact, some car sellers replace their old cars with pre-owned cars instead of buying new ones.

Unlike new cars, where price and supply are fairly deterministic and managed by OEMs (Original Equipment Manufacturer / except for dealership level discounts which come into play only in the last stage of the customer journey), used cars are very different beasts with huge uncertainty in both pricing and supply. Keeping this in mind, the pricing scheme of these used cars becomes important in order to grow in the market. As a senior data scientist at Cars4U, you have to come up with a pricing model that can effectively predict the price of used cars and can help the business in devising profitable strategies using differential pricing. For example, if the business knows the market price, it will never sell anything below it.

Objective

To explore and visualize the dataset, build a linear regression model to predict the prices of used cars, and generate a set of insights and recommendations that will help the business.

Data Description

The data contains the different attributes of used cars sold in different locations. The detailed data dictionary is given below.

Data Dictionary

  • S.No.: Serial number
  • Name: Name of the car which includes brand name and model name
  • Location: Location in which the car is being sold or is available for purchase (cities)
  • Year: Manufacturing year of the car
  • Kilometers_driven: The total kilometers driven in the car by the previous owner(s) in km
  • Fuel_Type: The type of fuel used by the car (Petrol, Diesel, Electric, CNG, LPG)
  • Transmission: The type of transmission used by the car (Automatic/Manual)
  • Owner: Type of ownership
  • Mileage: The standard mileage offered by the car company in kmpl or km/kg
  • Engine: The displacement volume of the engine in CC
  • Power: The maximum power of the engine in bhp
  • Seats: The number of seats in the car
  • New_Price: The price of a new car of the same model in INR Lakhs (1 Lakh INR = 100,000 INR)
  • Price: The price of the used car in INR Lakhs
We will start by following this methodology:  
  1. Data Collection: Begin by collecting a dataset that contains the input features and corresponding car prices. This dataset will be split into a training set (used to train the model) and a testing set (used to evaluate the model’s performance).
  2. Data Preprocessing: Clean and preprocess the data, addressing any missing values or outliers, and scaling the input features to ensure that they are on the same scale.
  3. Model Training: Train the linear regression model on the training dataset. This step involves finding the best-fitting line that minimizes the error between the actual and predicted house prices. Most programming languages, such as Python, R, or MATLAB, have built-in libraries that simplify this process.
  4. Model Evaluation: Evaluate the model’s performance on the testing dataset by comparing its predictions to the actual car prices. Common evaluation metrics for linear regression include Mean Absolute Error (MAE), Mean Squared Error (MSE), and R-squared.
  5. Model Optimization: If the model’s performance is unsatisfactory, consider feature engineering, adding more data, or using regularization techniques to improve the model’s accuracy.
The dataset used to build this model can be found by visiting my GitHub page (by clicking the like here).

Importing Libraries

Copy Code 


# Libraries to help with reading and manipulating data
import numpy as np
import pandas as pd

# Libraries to help with data visualization
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()

# Removes the limit for the number of displayed columns
pd.set_option("display.max_columns", None)
# Sets the limit for the number of displayed rows
pd.set_option("display.max_rows", 200)

#Train/Test/Split
from sklearn.model_selection import train_test_split # Sklearn package's randomized data splitting function

#Sklearn libraries
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from sklearn.preprocessing import OneHotEncoder

#Show all columns and randomize the row display
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 200)

Data Collection

This project was coded using Google Colab. The data was read directly from Google Drive.
Copy Code 


#mount and connect Google Drive
from google.colab import drive
drive.mount('/content/drive')

#Import dataset "used_cars_data.csv"
data = pd.read_csv('/content/drive/My Drive/Colab Notebooks/used_cars_data.csv')

Data Preprocessing

Data preprocessing is a crucial initial step in the machine learning process, aimed at providing a comprehensive understanding of the dataset at hand. By investigating the underlying structure, patterns, and relationships within the data, the analysis allows practitioners to make informed decisions about feature selection, model choice, and potential preprocessing requirements. This process often involves techniques such as data visualization, summary statistics, and correlation analysis to identify trends, detect outliers, and assess data quality. Gaining insights through data exploratory analysis not only helps in uncovering hidden relationships and nuances in the data but also aids in hypothesis generation and model validation. Ultimately, a thorough exploratory analysis sets the stage for building more accurate and reliable machine learning models, ensuring that the data-driven insights derived from these models are both meaningful and actionable. Review the Dataset
Copy Code 


#Sample of (10) rows
data.sample(10)
Next, we will look at the shape of the dataset:
Copy Code 


#Number of rows and columns
print(f'Number of rows: {data.shape[0]} and Number of columns: {data.shape[1]}')
We see from reviewing the shape that the dataset contains 7,253 rows and 14 columns. Additionally, we see that the index column is identical to the S. No column so we can drop this as it does not offer any value in our model:
Copy Code 


#Drop S.No. column
data.drop(['S.No.'], axis=1, inplace=True)
data.reset_index(inplace=True, drop=True)
Next, review the datatypes:
Copy Code 


#Review the datatypes
data.info()
The dataset contains the following datatypes:
  • (3) float64
  • (3) int64
  • (8) object
The following columns are missing data:
  • Engine: .6% of values are missing
  • Power: 2.4% of values are missing
  • Milage: 0.003% of values are missing
  • Seats: 0.73% of values are missing
  • Price: 17% of values are missing
We can also conduct a statistical analysis on the dataset by running:
Copy Code 


#Statistical analysis of dataset
data.describe().T
The results return the following: Year
  • Mean: 2013
  • Min: 1996
  • Max: 2019
Kilometers_Drive
  • Mean: 58699.06
  • Min: 171.00
  • Max: 6,500,000.00
Seats
  • Mean: 5.28
  • Min: 0.00
  • Max: 10.00
New_Price
  • Mean: 21.30
  • Min: 3.91
  • Max: 375.00
Price
  • Mean: 9.48
  • Min: 0.44
  • Max: 160.00
When checking for duplicates, we found there were three duplicated rows in the dataset. Since these do not add any additional value, we will move forward by eliminating these rows.
Copy Code 


#Check for duplicates
data.duplicated().sum()

#Dropping duplicated rows
data.drop_duplicates(keep ='first',inplace = True)


#Confirm duplicated are removed
data.duplicated().sum()
We are now ready to move to univariate analysis. We will start with the name column. Right off the bat, it was noticed that the dataset contains both the make and model names of the cars. For this analysis, we have elected to drop the model (Names) from our analysis.
Copy Code 


#Create a new column of make by separating it from the name
data['Make'] = data['Name'].str.split(' ').str[0]

#Dropping name column 
data.drop(['Name'], axis = 1, inplace=True) data.reset_index(inplace=True, drop=True)
Next, we will convert this datatype from an object to a category datatype:
Copy Code 


#Convert make column from object to category
data['Make'] = data['Make'].astype('category', errors = 'raise')

#Confirm datatype
data['Make'].dtype
Let’s evaluate the breakdown of each make by counting each and storing them in a new data frame:
Copy Code 


#How many values for each make
pd.DataFrame(data[['Make']].value_counts(ascending=False))
One thing that was noticed is that there are two categories for the make Isuzu. Let’s consolidate this into a single make:
Copy Code 


#Consolidate make Isuzu into one category
data.loc[data['Make'] == 'ISUZU','Make'] = 'Isuzu'
data['Make']= data['Make'].cat.remove_categories('ISUZU')
To visualize the make category breakdown:
Copy Code 


#Countplot of the make column
plt.figure(figsize = (30,8))
ax = sns.countplot(x = 'Make', data = data)
ax.set_xticklabels(ax.get_xticklabels(), rotation = 90);
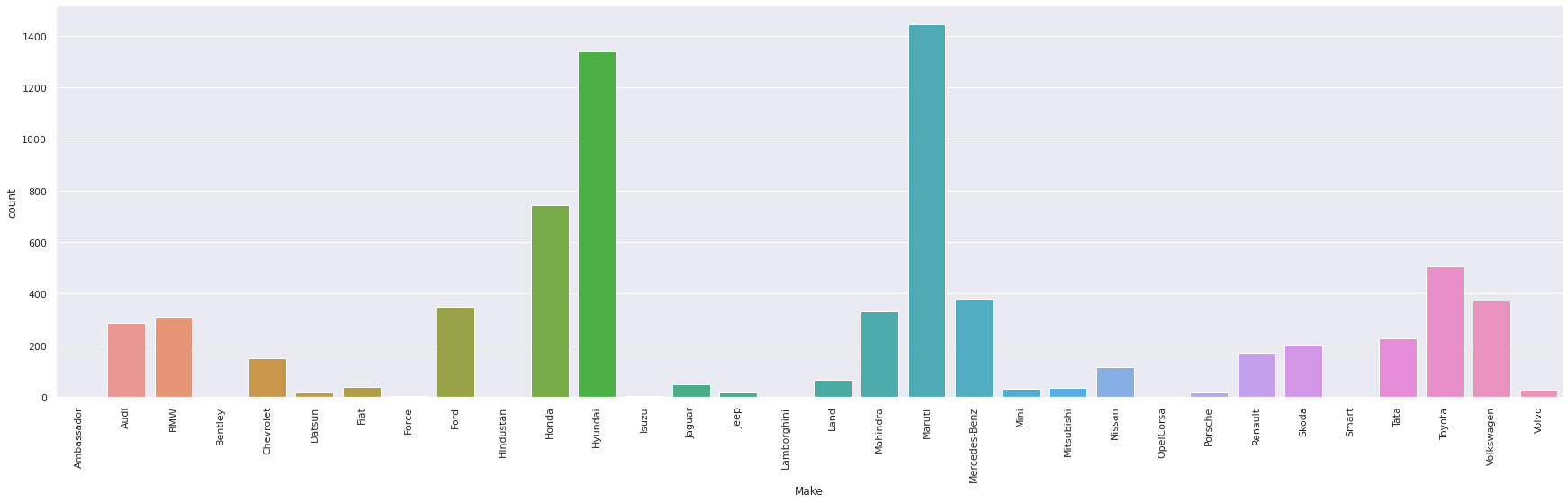The top five makes based on the results are:
  • Maruti: 1404
  • Hyundai: 1284
  • Honda: 734
  • Toyota: 481
  • Mercedes-Benz: 378
Let’s now explore the price data. The first thing we validated is whether or not there were NULL values in the price category. After evaluation, we identified 1,233 values that were missing. To fix this, we replaced the NULL values with the median price of the cars.
Copy Code 


#Missing data for price
data['Price'].isnull().sum()
     
#Replace NaN values in the price column with the median
data['Price'] = pd.DataFrame(data['Price'].fillna(int(data['Price'].median())))
When looking at a frequency dataframe, we see that the most common price identified was 5 lakhs (or approximately $6,115 USD).
Copy Code 


#Review the price breakdown
pd.set_option('display.max_rows', 10)
pd.DataFrame(data['Price'].value_counts(ascending=False))
We also were able to conduct a statistical analysis to find the prices range from 0.44 – 160 lakhs with a mean price is 8.72.
Copy Code 


#Statistical analysis of price
pd.DataFrame(data['Price']).describe().T
Here is a breakdown of the average price of the cars by make:
Copy Code 


#Average price of cars by make
avg_price = data.groupby(['Make'])['Price'].mean().fillna(0).sort_values(ascending= False).index
#catplot of make and price
sns.catplot(x = "Make", y = "Price", data = data, kind = 'bar', height = 7, aspect = 2, order = avg_price).set(title = 'Price by Make') 
plt.xticks(rotation=90);
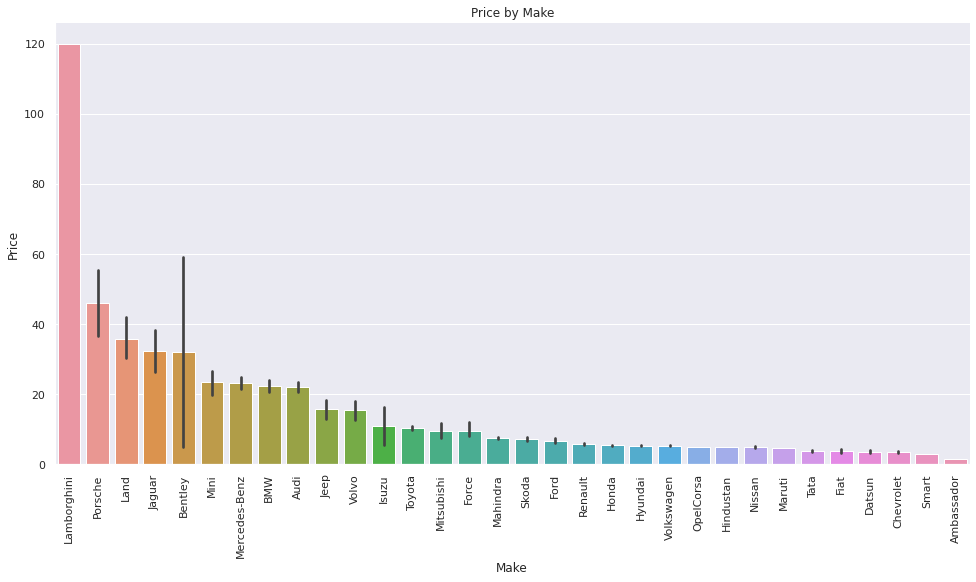It is interesting to note the difference between the average cost of new cars of the same make and the used cars available at Cars4U:
Copy Code 


#Average new price of cars by make 
avg_new_price = data.groupby(['Make'])['New_Price'].mean().fillna(0).sort_values(ascending= False).index 

#catplot of make and new price 
sns.catplot(x = "Make", y = "New_Price", data = data, kind = 'bar', height = 7, aspect = 2, order = avg_new_price ).set(title = 'New Price by Make') plt.xticks(rotation=90);
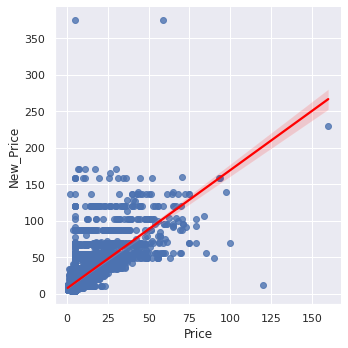
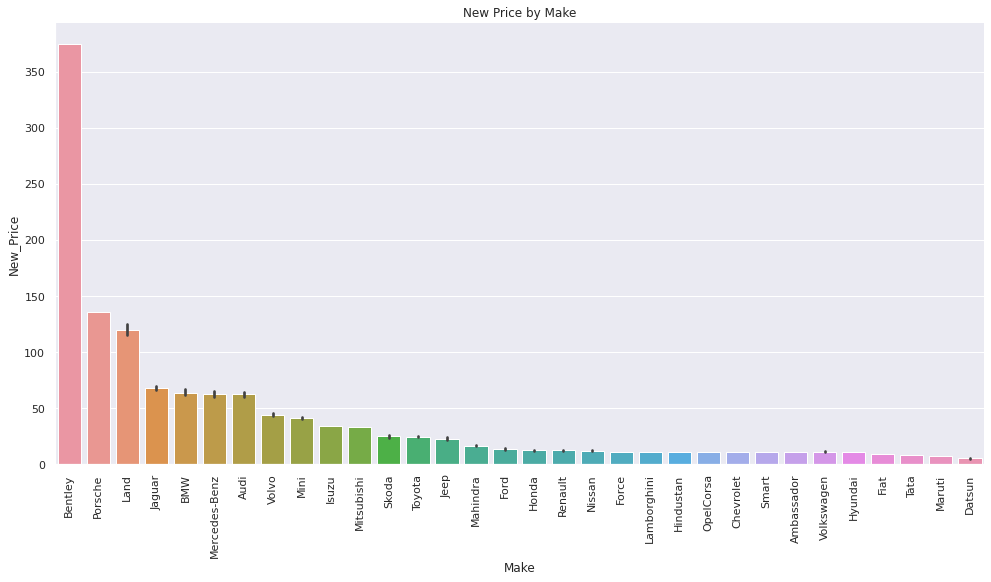We can see that there is a moderate positive correlation between the price of a new car and the price of the cars at Cars4U:
Copy Code 


#Correlation between price and new price
data[['New_Price', 'Price']].corr()
Next, we converted the transmission data to categorical data and reviewed the breakdown between automatic and manual transmission cars:
Copy Code 


#Convert Transmission column from object to category
data['Transmission'] = data['Transmission'].astype('category', errors = 'raise')

#Displot of the transmission column
plt.figure(figsize = (8,8))
sns.displot(x = 'Transmission', data = data);

#Specific value counts for each transmission types
pd.DataFrame(data[‘Transmission’].value_counts(ascending=False))
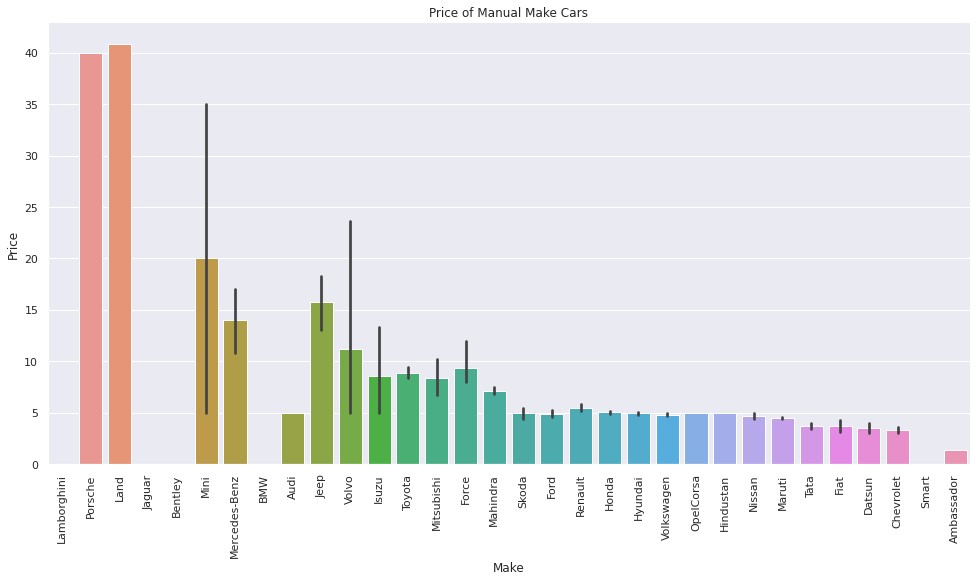
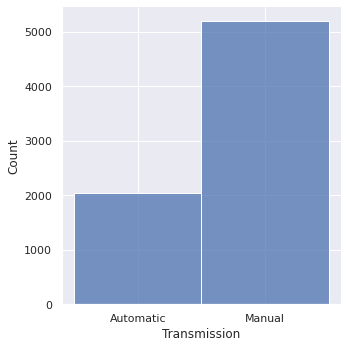As we see from the distribution plot below, manual transmission cars account 71.8% of the cars –  far more than automatic transmission cars at Cars4U. When evaluating the average cost of the cars with manual transmissions for new and used cars, we identified a 44.3% difference in prices:
Copy Code 


#Average price of cars by make with manual transmissions
man_price = data.groupby(['Make'])['Price'].mean().fillna(0).sort_values(ascending= False).index
#catplot of make and price for all manual transmissions
sns.catplot(x = "Make", y = "Price", data = manual, kind = 'bar', height = 7, aspect = 2, order = man_price).set(title = 'Price of Manual Make Cars') 
plt.xticks(rotation=90);

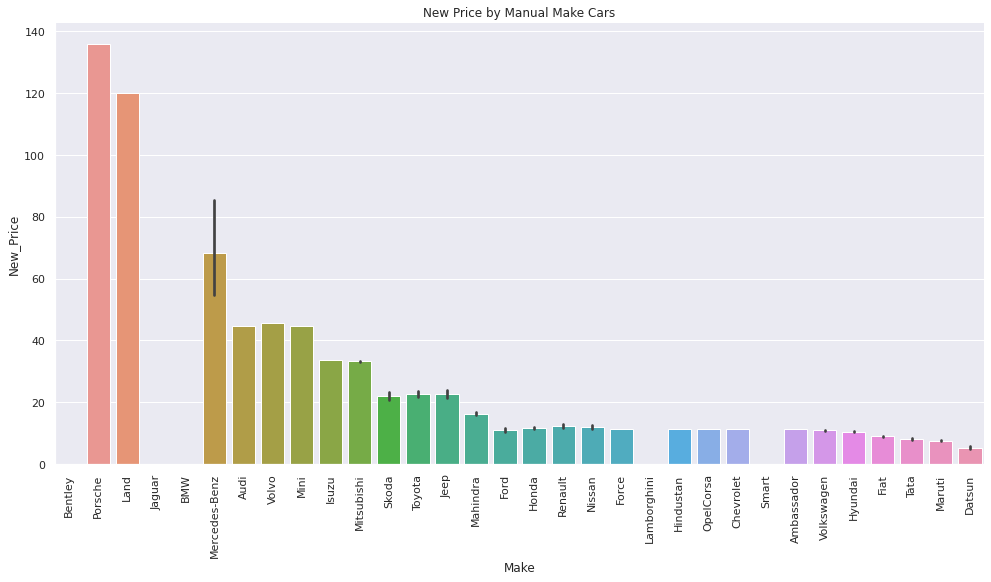
#Average new price of cars by make with manual transmissions
man_cars = data.groupby(['Make'])['New_Price'].mean().fillna(0).sort_values(ascending= False).index
#catplot of make and price for all manual transmissions
sns.catplot(x = "Make", y = "New_Price", data = manual, kind='bar', height=7, aspect=2, order= man_cars).set(title = 'New Price by Manual Make Cars') 
plt.xticks(rotation=90);

#Difference between the mean price and mean new price of manual cars
manual['Price'].mean()/manual['New_Price'].mean()
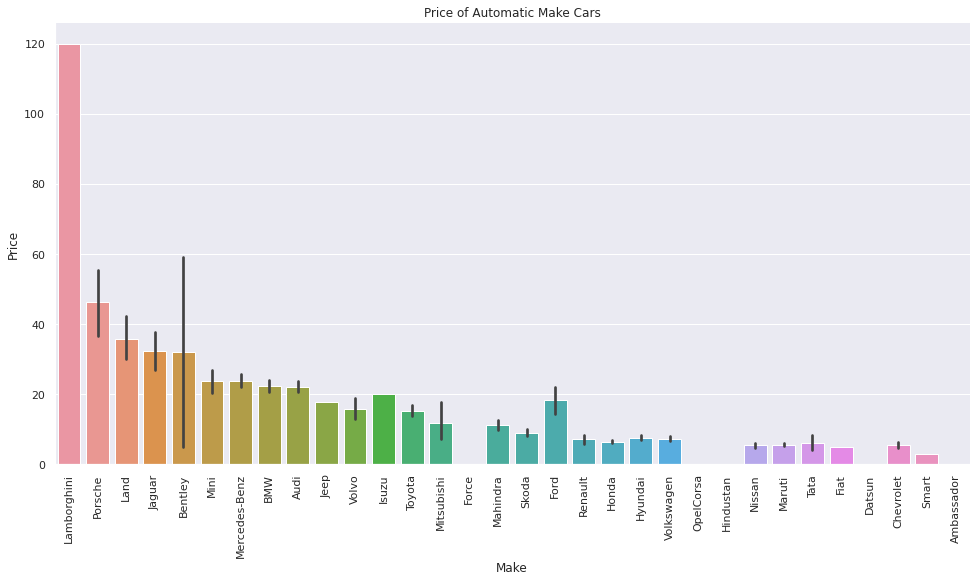
  It is interesting to note that there is a smaller difference in price between used and new car prices for cars with automatic transmissions – a difference of only 38.7%.
Copy Code 


#Average price of cars by make with automatic transmissions 
auto_price = data.groupby(['Make'])['Price'].mean().fillna(0).sort_values(ascending= False).index 

#catplot of make and price for all automatic transmissions 
sns.catplot(x = "Make", y = "Price", data = automatic, kind = 'bar', height = 7, aspect = 2, order = auto_price).set(title = 'Price of Automatic Make Cars') plt.xticks(rotation=90); 

#Average new price of cars by make automatic transmissions 
new_auto = data.groupby(['Make'])['New_Price'].mean().fillna(0).sort_values(ascending= False).index #catplot of make and new price for all automatic transmissions sns.catplot(x = "Make", y = "New_Price", data = automatic, kind = 'bar', height = 7, aspect = 2, order = new_auto).set(title = 'New Price of Automatic Make Cars') plt.xticks(rotation=90); #Difference between the mean price and mean new price of automatic cars automatic['Price'].mean()/automatic['New_Price'].mean()
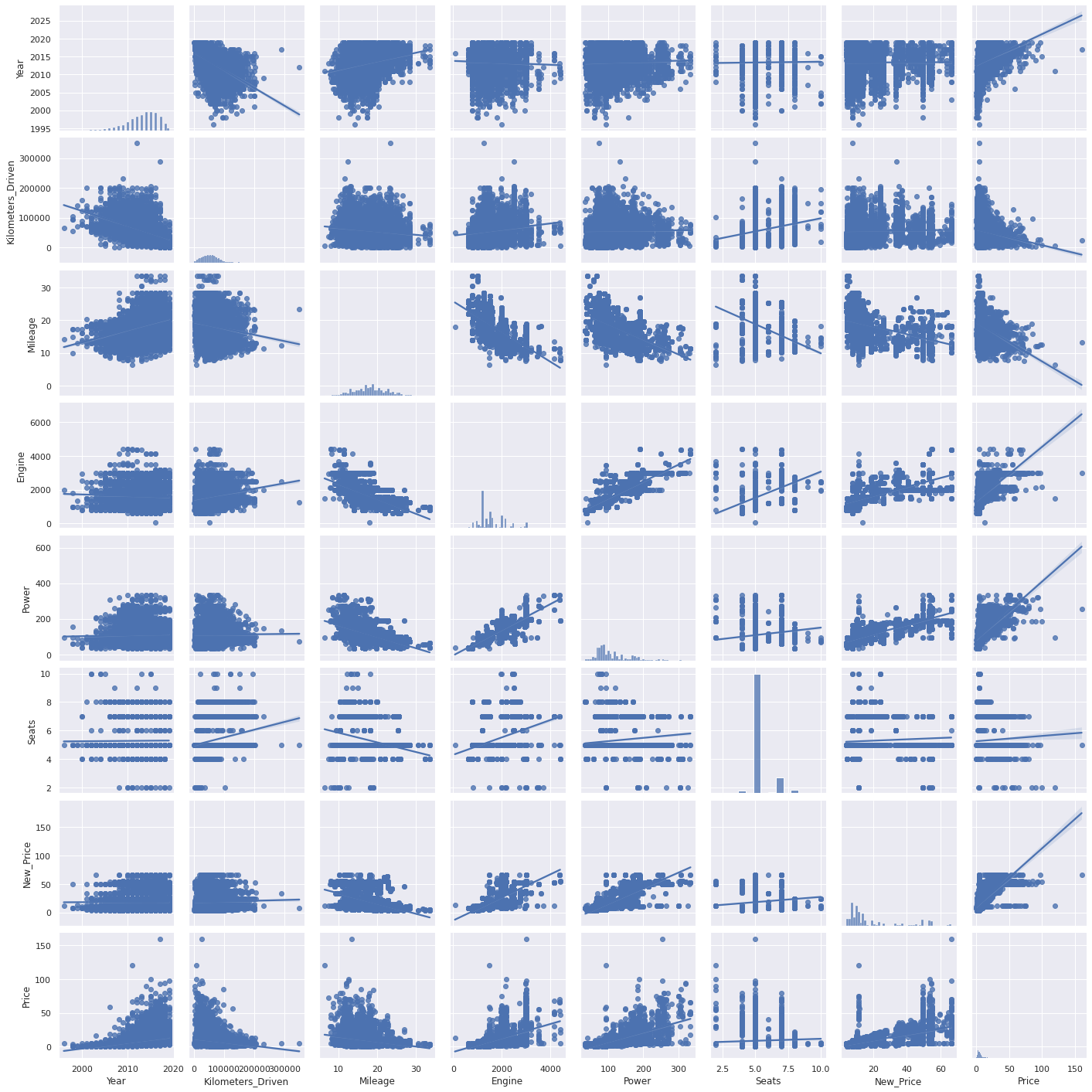
There are other features that we can explore in our exploratory data analysis (all of which you can view on the GitHub repo found here, but we will now evaluate the correlation between all these features to help identify the strength of their relationships. One thing that is important to keep in mind when completing the data analysis is the ensure that all features containing NaN or have no data are either dropped or imputed. It is also important to treat any outliers that could potential skew your dataset and have an adverse impact on your model metrics. For example, the power feature contained a number of outliers that we treated by first converting them to NaN values with NumPy and replacing them with the median central tendency:
Copy Code 


#Treating the outliers for power
power_outliers = [340., 360., 362.07, 362.9, 364.9, 367., 382., 387.3, 394.3, 395., 402., 421., 444., 450., 488.1,  
                   500., 503., 550., 552., 560., 616.]
data['Power_Outliers'] = data['Power']
#Replacing the power values with np.nan
for outlier in power_outliers:
    data.loc[data['Power_Outliers'] == outlier, 'Power_Outliers'] = np.nan
data['Power_Outliers'].isnull().sum()

#Group the outliers by Make and impute with median
data['Power_Outliers'] = data.groupby(['Make'])['Power_Outliers'].apply(lambda fix : fix.fillna(fix.median()))
data['Power_Outliers'].isnull().sum()
#Transfer new data back to original column
data['Power'] = data['Power_Outliers']
#Drop Power_Outliers since it is no longer needed
data.drop(['Power_Outliers'], axis=1, inplace=True)
data.reset_index(inplace=True, drop=True)
You could also choose to drop missing data if the dataset is large enough, however, this should be done with caution as to not impact the results of your models as this could lead to underfitting. Underfitting occurs when a machine learning model fails to capture the underlying patterns in the data, resulting in poor performance on both the training set and the test set. This usually happens when the model is too simple, or when there is not enough data to train the model effectively. To avoid underfitting, it’s important to ensure that your dataset is large enough and diverse enough to capture the complexities of the problem you’re trying to solve. Additionally, use an appropriate model complexity that is neither too simple nor too complex for your data. You can also leverage techniques like cross-validation to get a better estimate of your model’s performance on unseen data. Below is a pair plot that highlights the strength of the relationships for all possible bivariate relationships: Here is a heat map of the correlations represented above:  
To better improve our model. we have performed log transformations on our price feature. Log transformations are a common preprocessing technique used in machine learning to modify the distribution of data features. They can be particularly useful when dealing with data that has a skewed distribution, as log transformations can help make the data more normally distributed, which can improve the performance of some machine learning algorithms. The main reasons for using log transformations are:
  1. Reduce skewness: Log transformations can help reduce the skewness of the data by compressing the range of large values and expanding the range of smaller values. This helps in transforming a skewed distribution into a more symmetrical, bell-shaped distribution, which is often assumed by many machine learning algorithms.
  2. Stabilize variance: In some cases, the variance of a dataset may increase with the magnitude of the data. Log transformations can help stabilize the variance by reducing the impact of extreme values, making the data more homoscedastic (having a constant variance).
  3. Improve interpretability: When dealing with data that spans several orders of magnitude, log transformations can make the data more interpretable by converting multiplicative relationships into additive ones. This can be particularly useful for understanding the relationship between variables in regression models.
  4. Enhance algorithm performance: Many machine learning algorithms, such as linear regression, assume that the input features have a normal (Gaussian) distribution. Applying log transformations can help meet these assumptions, leading to better algorithm performance and more accurate predictions.
  5. Handle multiplicative effects: Log transformations can help model multiplicative relationships between variables, as the logarithm of a product is the sum of the logarithms of its factors. This property can help simplify complex relationships in the data and make them easier to model.
Keep in mind that log transformations are not suitable for all types of data, particularly data with negative values or zero, as the logarithm is undefined for these values. Additionally, it’s essential to consider the specific machine learning algorithm and the nature of the data before deciding whether to apply a log transformation or another preprocessing technique. Below was the log transformation performed on our price feature:
Copy Code 


#Create log transformation columns
data['Price_Log'] = np.log(data['Price'])
data['New_Price_Log'] = np.log(data['New_Price'])
data.head()
Notice how the distribution is now much more balanced and naturally distributed: The last step in our data preprocessing step is to use one-hot encoding on our categorical variables. One-Hot Encoding is a technique used in machine learning to convert categorical variables into a binary representation that can be easily understood and processed by machine learning algorithms. Categorical variables are those that take on a limited number of distinct categories or levels, such as gender, color, or type of car. Most machine learning algorithms require numerical input, so converting categorical variables into a numerical format is a crucial preprocessing step. The one-hot encoding process involves creating new binary features for each unique category in a categorical variable. Each new binary feature represents a specific category and takes the value 1 if the original variable’s value is equal to that category, and 0 otherwise. Here’s a step-by-step explanation of the one-hot encoding process:
  1. Identify the categorical variable(s) in your dataset.
  2. For each categorical variable, determine the unique categories.
  3. Create a new binary feature for each unique category.
  4. For each instance (row) in the dataset, set the binary feature value to 1 if the original variable’s value matches the category represented by the binary feature, and 0 otherwise.
For example, let’s say you have a dataset with a categorical variable ‘Color’ that has three unique categories: Red, Blue, and Green. To apply one-hot encoding, you would create three new binary features: ‘Color_Red’, ‘Color_Blue’, and ‘Color_Green’. If an instance in the dataset has the value ‘Red’ for the original ‘Color’ variable, then the binary features would be set as follows: ‘Color_Red’ = 1, ‘Color_Blue’ = 0, and ‘Color_Green’ = 0. The advantages of using this technique are:
  1. It creates a binary representation that is easy for machine learning algorithms to process and interpret.
  2. It does not impose an ordinal relationship between categories, which may not exist in the original data.
There are some drawbacks of one-hot encoding as well. These include:
  1. It can lead to a large increase in the number of features, especially when dealing with categorical variables with many unique categories. This can increase memory usage and computational time.
  2. It does not capture any relationship between categories, which may be present in some cases.
To mitigate these drawbacks, you can consider using other encoding techniques, such as target encoding or ordinal encoding, depending on the specific nature of the categorical variables and the machine learning algorithm being used, however for this model, one-hot encoding is our best option.
Copy Code 


#One-hot encoding our variables
data = pd.get_dummies(data, columns=['Location', 'Fuel_Type','Transmission','Owner_Type','Make'], drop_first=True)
We are now ready to start building our models.

Model Training, Model Evaluation, and Model Optimization

The first model we will build contains the log transformation of the Price and New Price features using one-hot Encoding. The dependent variable is Price.
Copy Code 


#Select Independent and Dependent Variables
a = data1.drop(['Price'], axis=1)
b = data1["Price"]
Next, we will split the dataset into training and testing, respectfully, using a 70/30 split:
Copy Code 


#Splitting the data in 70:30 ratio for train to test data
a_train, a_test, b_train, b_test = train_test_split(a, b, test_size=0.30, random_state=1)

#View split
print(“Number of rows in train data =”, a_train.shape[0]) print(“Number of rows in test data =”, a_test.shape[0])
Here, we see that the training dataset contains 5,076 rows and the testing data contains 2,176 rows.
We now apply linear regression to the training set and fit the model:
Copy Code 


#Fit model_one
model_one = LinearRegression()
model_one.fit(a_train, b_train)
We can now evaluate the model performance on both the training and the testing dataset. In evaluating a supervised learning model using linear regression, there are several metrics that can be used to measure its performance. However, the most commonly used and valuable metric is the Root Mean Squared Error (RMSE). RMSE is calculated as the square root of the mean of the squared differences between the predicted and actual values. It provides an estimate of the average error in the predictions and is particularly useful because it is in the same units as the target variable. A lower RMSE value indicates a better fit of the model to the data. Other metrics that can be used to evaluate a linear regression model include Mean Absolute Error (MAE), Mean Squared Error (MSE), and R-squared (R²), but RMSE is often preferred due to its interpretability and sensitivity to larger errors in the predictions.
Copy Code 


#Checking model performance on train set
print("Training Performance")
print('\n')
training_perfomace_1 = model_performance_regression(model_one, a_train, b_train)
training_perfomace_1

#Checking model performance on test set
print("Test Performance")
print("\n")
test_performance_1 = model_performance_regression(model_one, a_test, b_test)
test_performance_1
Training Data Results for Model 1
Testing Data Results for Model 1
Let’s summarize what this all means. The model appears to perform reasonably well based on the R-squared and adjusted R-squared values. An R-squared value of 0.797091 suggests that the model explains approximately 79.7% of the variance in the data. This indicates that the model has captured a significant portion of the underlying relationship between the features and the target variable (used car prices). This is generally a good sign. Additionally, the fact that the adjusted R-squared is close to the R-squared value indicates that the model has not likely overfit the data, which is a good sign. However, A MAPE of 66.437161% indicates that the model’s predictions are, on average, off by 66.44%. This value seems high and might not be ideal for accurately predicting used car prices. A lower MAPE would be desired.
Next, we will evaluate the coefficients and intercept of our first model. The coefficients and intercepts play a crucial role in understanding the relationship between the input features and the target variable. Evaluating the coefficients and intercepts provides insights into the model’s behavior and helps in interpreting the results. Since the coefficients of a linear regression model represent the strength and direction of the relationship between each independent variable and the dependent variable, a positive coefficient indicates that as the feature value increases, the target variable also increases, while a negative coefficient suggests the opposite. The intercept represents the expected value of the target variable when all the independent variables are zero. By examining the coefficients and intercept, we can better understand the relationships between the variables and how they contribute to the model’s predictions. Additionally, evaluating the coefficients can help us determine the relative importance of each feature in the model. Features with higher absolute coefficients have a more significant impact on the target variable, while features with lower absolute coefficients have a smaller impact. This can help in feature selection and reducing model complexity by eliminating less important features.
Examining the coefficients and intercept can also help to identify potential issues with the model, such as multicollinearity, which occurs when two or more independent variables are highly correlated. Multicollinearity can lead to unstable coefficient estimates, making it difficult to interpret the model. Checking the coefficients for signs of multicollinearity can help in model validation and improvement.
Copy Code 


#Coefficients and intercept of model_one
coef_data_1 = pd.DataFrame(np.append(model_one.coef_, model_one.intercept_), index=a_train.columns.tolist() + ["Intercept"], columns=["Coefficients"],)
coef_data_1
Let’s identify the feature importance. Identifying the most important features can help in interpreting the model and understanding the relationships between input features and the target variable.  This can provide insights into the underlying structure of the data and help in making informed decisions based on the model’s predictions. Evaluating feature importance can guide the process of feature selection, which involves choosing a subset of features to include in the model. By selecting only the most important features, you can reduce model complexity, improve model performance, and reduce the risk of overfitting. By focusing on the most important features, the model can often achieve better performance, as it will be less influenced by noise or irrelevant information from less important features. This can lead to more accurate and robust predictions.
Copy Code 


#Evaluation of Feature Importance
imp_1 = pd.DataFrame(data={
    'Attribute': a_train.columns,
    'Importance': model_one.coef_
})
imp_1 = imp_1.sort_values(by='Importance', ascending=False)
imp_1
The five most important features in this model were:
  • Price_Log
  • Make_Porsche
  • Make_Bentley
  • Owner_Type_Third
  • Location_Jaipur
The output of a supervised learning linear regression mode represents the predicted value of the target variable based on the input features. Linear regression models establish a linear relationship between the input features and the target variable by estimating coefficients for each input feature and an intercept term. A linear regression model can be represented by the following equation: y = β0 + β1 * x1 + β2 * x2 + … + βn * xn + ε Where:
  • y is the predicted value of the target variable
  • β0 is the intercept (also known as the bias term)
  • β1, β2, …, βn are the coefficients for each input feature (x1, x2, …, xn)
  • ε is the residual error term
To find our output for this model:
Copy Code 


#Equation of linear regression
equation_one = "Price = " + str(model_one.intercept_)
print(equation_one, end=" ")

for i in range(len(a_train.columns)):
    if i != len(a_train.columns) - 1:
        print("+ (", model_one.coef_[i],")*(", a_train.columns[i],")",end="  ",)
    else:
        print("+ (", model_one.coef_[i], ")*(", a_train.columns[i], ")")
The following is the equation that represents model one:
Price = 736.4497985737344 + ( -0.3625329082148889 )*( Year ) + ( -1.3110189822674006e-05 )*( Kilometers_Driven ) + ( -0.014157293529257167 )*( Mileage ) + ( 0.0003911564010086188 )*( Engine ) + ( 0.0327950392035401 )*( Power ) + ( -0.3552105386835278 )*( Seats ) + ( 0.3012600646220953 )*( New_Price ) + ( 10.937580127939356 )*( Price_Log ) + ( -7.378205154754799 )*( New_Price_Log ) + ( 0.3734729001231947 )*( Location_Bangalore ) + ( 0.7548562308270204 )*( Location_Chennai ) + ( 0.7999091213003968 )*( Location_Coimbatore ) + ( 0.27342183503313544 )*( Location_Delhi ) + ( 0.566644864147059 )*( Location_Hyderabad ) + ( 1.2909791398995183 )*( Location_Jaipur ) + ( 0.31157631469545244 )*( Location_Kochi ) + ( 0.9662064166581987 )*( Location_Kolkata ) + ( 0.0339777741750662 )*( Location_Mumbai ) + ( 1.0204222416751427 )*( Location_Pune ) + ( -0.3802091756062127 )*( Fuel_Type_Diesel ) + ( 0.18076487651952045 )*( Fuel_Type_Electric ) + ( -0.23908062444603218 )*( Fuel_Type_LPG ) + ( 0.27479225149571107 )*( Fuel_Type_Petrol ) + ( 1.2895155610839053 )*( Transmission_Manual ) + ( -0.6766933399232838 )*( Owner_Type_Fourth & Above ) + ( 0.10616965362982267 )*( Owner_Type_Second ) + ( 1.8529146407467167 )*( Owner_Type_Third ) + ( -6.488302833289815 )*( Make_Audi ) + ( -7.248203698331185 )*( Make_BMW ) + ( 4.325350474691585 )*( Make_Bentley ) + ( -4.038107102236865 )*( Make_Chevrolet ) + ( -7.031021026543664 )*( Make_Datsun ) + ( -5.59999853972966 )*( Make_Fiat ) + ( -10.649089020356758 )*( Make_Force ) + ( -5.908256723880932 )*( Make_Ford ) + ( -14.022172786577073 )*( Make_Hindustan ) + ( -7.413408671437291 )*( Make_Honda ) + ( -6.624881118200216 )*( Make_Hyundai ) + ( -6.507350534989778 )*( Make_Isuzu ) + ( -2.7579382943766286 )*( Make_Jaguar ) + ( -7.237209350843373 )*( Make_Jeep ) + ( 1.021405182655144e-13 )*( Make_Lamborghini ) + ( 0.6875657149109964 )*( Make_Land ) + ( -6.862601073861168 )*( Make_Mahindra ) + ( -6.779191869062652 )*( Make_Maruti ) + ( -5.591474811962323 )*( Make_Mercedes-Benz ) + ( -3.422890916260733 )*( Make_Mini ) + ( -7.499324771098843 )*( Make_Mitsubishi ) + ( -5.870105956961656 )*( Make_Nissan ) + ( -1.3322676295501878e-13 )*( Make_OpelCorsa ) + ( 8.078157385327632 )*( Make_Porsche ) + ( -6.786208193728582 )*( Make_Renault ) + ( -6.497601071344171 )*( Make_Skoda ) + ( -4.837208865996979 )*( Make_Smart ) + ( -4.465909397072464 )*( Make_Tata ) + ( -6.9742671868802075 )*( Make_Toyota ) + ( -6.77936744766909 )*( Make_Volkswagen ) + ( -9.147868944835512 )*( Make_Volvo )
  Lastly, we will evaluate the PolynomialFeatures transformation to capture non-linear relationships between input features and the target variable. By introducing polynomial features, we can model these non-linear relationships and improve the performance of the linear regression model. PolynomialFeatures transformation works by generating new features from the original input features through polynomial combinations of the original features up to a specified degree. For example, if the original features are [x1, x2], and the specified degree is 2, the transformed features would be [1, x1, x2, x1^2, x1*x2, x2^2].
Copy Code 


#PolynomialFeatures Transformation
poly = PolynomialFeatures(degree=2, interaction_only=True)
a_train2 = poly.fit_transform(a_train)
a_test2 = poly.fit_transform(a_test)
poly_clf = linear_model.LinearRegression()
poly_clf.fit(a_train2, b_train)
print(poly_clf.score(a_train2, b_train))
The polynomial transformation improved the model from .79 to .97. These ten models (to see the remaining nine models, check out my notebook on GitHub) helped us to identify some key takeaways and recommendations for the business. Lower end cars had more of a negative impact on the price. Dealerships should look for more mid-ranged valued cars for more of an impact on sales. Another key point is that while the majority of the cars in the dataset are of petrol and diesel fuel types, electric cars had a positive effect on the price model. This is a good opportunity for dealers to start offering more selections in the electric car market – especially since fuel prices continue to rise. In many of the models built, Location_Kolkata had a negative effect on price. Furthermore, we also observed there was a good correlation between price and new price. Given this relationship, it is wise for the dealerships to understand that as the price of new cars get higher, used car prices can also increase. Secondly, both the mileage and kilometers driven have an inverse relationship – as the mileage and kilometers increase, the price drops. This makes sense as buyers are seeking cars that offer km/kg and have less mileage. Customers should expect to pay more for these cars. The recommendations are pragmatic. The best performing model used the log of price. In reality, this will mean nothing to the sales people. Dealers should look to:
  • Coimbatore, Banglore, and Kochi are locations that have the highest mean price for cars sold. Dealerships using these models should seek to increase marketing efforts here to increase sales. Accordingly, they should evaluate whether locations that have a negative impact on price (such as Kolkata) should remain open.
  • Offer more of an inventory of electric cars at the Coimbatore, Banglore, and Kochias locations. This had a positive impact on price.
  • Cars 2016-newer yield higher prices, but many customers have cars that are between 2012-2015. Look to load your inventory with cars that are only 2012 or newer as these are the most desirable.
  • While more customers have manual transmission cars, automatic cars almost always yield higher prices.
  • Since traffic is always a pain point, acquiring more automatic cars (which are also more fuel efficient) will increase price.
  • Dealerships should look to acquire makes like Maruti, Hyundai,  and Honda’s as these are the most popular selling brands.
artificial intelligencelinear regressionmachine learningsupervised learning
By Artificial Intelligence, Linear Regression, Machine Learning, Supervised LearningLeave a Comment on Unleashing the Power of Linear Regression in Supervised Learning

Leave a Reply

Your email address will not be published. Required fields are marked *